A logistic regression example

Before moving on let's try a different type of regression: logistic regression. Unlike linear regression, which models a continuously varying outcome variable (such as expression levels), logistic regression models a binary 0/1 outcome - or more generally binomial (count) or multinomial (categorical) outcome.

Prerequisites

To get started, download the file 'o_bld_group_data.csv' from [this folder](The data can be found in this folder - and place it in your folder. E.g. from the command line:

curl -O https://raw.githubusercontent.com/chg-training/chg-training-resources/main/docs/statistical_modelling/regression_modelling/data/o_bld_group_data.tsv

(Or use the direct link.)

Now load it into your R session:

data = read_delim( "o_bld_group_data.tsv", delim = "\t" )

What's in the data?

The data contains genotype calls for the genetic variants rs8176719 and rs8176746, measured in a set of severe malaria cases and population controls from several African countries. These variants lie in the ABO gene and together encode the most common ABO blood group types.

The data were collected by seperatecase-control studies operating in each country and were genotyped by MalariaGEN. They were described in this paper.

Before starting explore the data (e.g. using View(), table() and so on) and make sure you know what is in there. You should see:

• Information on the sample identifier and sex, and ethnicity

• The status column, which indicates if the sample was collected as a case (i.e. came into hospital with severe symptoms of malaria) or a control

• A column with the rs8176719 genotypes and one with the rs8176746 genotypes.

• And some columns marked PC_1 - PC_5.

Warm-up question

O blood group is encoded by a homozygous deletion (-/- at rs8176719). What is the frequency of O blood group in this sample in each population?

In non-O individuals, B blood group is encoded by the 'T' allele of rs8176746. What is the frequency of B blood group in non-O-blood group individuals in each country?

If you want to see what the genetic effect of these variants is, I highly recommend looking it up in the UCSC genome browser and/or the Ensembl genome browser . You should see that rs8176719 is a frameshift variant within ABO gene. (Which exon is it in?). Chromosomes with the deletion allele (like the GRCh38 reference sequence) produce a malformed enzyme that prevents synthesis of A or B antigens (they cause a loss of glycosyltransferase activity).

(Of course, humans have two copies so if the sample is heterozygous then it's quite possible the other copy does express A or B.)

Question

If you have time - figure out where rs8176746 is and what effect it has on the protein. (E.g. you can do this by zooming into the variant in the UCSC browser, figuring out the amino acid sequence (remembering that it is transcribed on the reverse strand), and comparing this to a table of the genetic code.

Running the regression

A and B antigens are bound to the surface of red cells and tend to stick to things - it's plausible malaria parasites might exploit this. Let's therefore use this data to test to see if O blood group is associated with malaria status.

To get started let's create a new variable indicating 'O' blood group status:

data$o_bld_group = NA           # in case any rs8176719 genotypes are missing
data$o_bld_group[ data$rs8176719 == '-/-' ] = 1
data$o_bld_group[ data$rs8176719 == '-/C' ] = 0
data$o_bld_group[ data$rs8176719 == 'C/C' ] = 0

Also - for best results let's make sure our status variable is coded the right way round (with "CONTROL" as the baseline):

data$status = factor( data$status, levels = c( "CONTROL", "CASE" ))

Running a logistic regression is very much like a linear regression, except we use glm in place of lm:

fit = glm(
    status ~ o_bld_group,
    data = data,
    family = "binomial"  # needed to specify logistic regression
)

As before we can now see the coefficients:

summary(fit)$coeff

Woah. The estimate is $-0.334 / 0.039 = 8.6$ standard errors from zero!

Including covariates.

But wait! Just as before there are some covariates in the data.

Here there is one covariate we should definitely include: the country. This is because the samples were collected as a case/control study seperately in each country. For all we know there were different sampling strategies or with difference numbers of cases/controls. Maybe this is skewing results?

fit2 = glm(
    status ~ o_bld_group + country,
    data = data,
    family = "binomial"  # needed to specify logistic regression
)
summary(fit2)$coeff

Note

Compare the names of the outcome parameters, with the set of countries in the data. Do you notice anything?

This illustrates the way that regression handles categorical variables like the country by default. One country is chosen as a 'baseline' (in an ad hoc manner) and the variation in the other countries are measured against it. Which country did glm pick as the baseline here? Which countries have higher O blood group frequencies and which have lower?

Note

If you want to control which country is the baseline, turn the column into a factor with the right ordering. For example let's order countries roughly west-to-east:

data$country = factor(
    data$country,
    levels = c(
        "Gambia",
        "Ghana",
        "Cameroon",
        "Tanzania",
        "Kenya"
    )
)

Now re-run the regression - can you see the difference?

What about ethnicity? For example maybe O blood group is more common in some ethnic groups, and those happen to be less prone to getting severe malaria or less likely to get enrolled in the study?

fit3 = glm(
    status ~ o_bld_group + country + ethnicity,
    data = data,
    family = "binomial"  # needed to specify logistic regression
)
summary(fit3)$coeff

Note

This produces a long output! Make sure you know what it's showing.

We could also try the principal components as well. They are computed from genome-wide genotypes and reflect population structure in each country. Because of the way these have been computed (seperately in each country) the right way to include them is using an interaction term. E.g. for the first principal component:

fit4 = glm(
    status ~ o_bld_group + country + country * PC_1,
    data = data,
    family = "binomial"  # needed to specify logistic regression
)
summary(fit4)$coeff

Can you 'destroy' the association by including covariates?

Question

Which of these statements do you agree with:

• O blood group is associated with lower chance of having severe malaria, relative to A/B blood group.
• O blood group is associated with higher chance of having severe malaria, relative to A/B blood group.
• O blood group is protective against severe malaria.
• We can't tell if O blood group is protective or confers risk against severe malaria.

Interpreting the parameters

The basic model

The logistic regression model is similar to the linear regression model, but a bit more complex at first sight. It works like this: start with same linear predictor as for linear regression:

$$\mu + \beta \times \text{genotype} + \gamma \times \text{covariate} + ...$$

...but now instead of modelling the outcome directly as in linear regression...

$$Y = \text{linear predictor} + \text{noise}$$

...we first transform the predictor through the logistic function.

$$\text{logistic}(x) = \frac{e^x}{1+e^x}$$

We then model the outcome by saying that the *probability that the outcome is a "CASE" is equal to the logistic function of the linear predictor:

$$\text{probability}(Y=1) = \text{logistic}( \mu + \beta \times \text{genotype} + \gamma \times \text{covariate} + ... )$$

...where I'm imagining $Y=1$ as indicating a case and $Y=0$ a control.

In this way the model provides a probabalistic model suitable for a binary outcome variable, but still using the same underlying predictor on the linear scale.

The logistic and logit functions

To get a better sense of how this works, plot the logistic function:

logistic <- function(x) {
    exp(x) / ( 1 + exp(x) )
}
x = seq( from= -6, to = 6, by = 0.01 )
plot_data = tibble(
    x = x,
    probabiy = logistic(x)
)
print(
    ggplot( data = plot_data, aes( x = x, y = y ))
    + geom_line()
    + geom_vline( xintercept = 0, linetype = 2, col = 'red' )
)

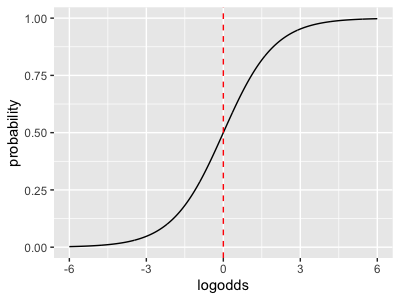
The logistic function maps the real line (x axis, where the linear predictor lives) onto the unit interval $(0,1)$ (y axis). In principle $+\infty$ is mapped onto 1 and $-\infty$ to $0$. As in the above plot, we interpret this as mapping log odds space onto the space of probabilities. Why do we say "log odds" here? To see this, it's easiest to think about the inverse function to the logistic function. This is the logit function and can be written:

$$\text{logit}(p) = \log \left( \frac{p}{1-p} \right)$$

The logit function specifically computes the logarithm of the odds associated to a probability p.

Challenge

Plot $\text{logit}$ as well. It should look something like this:

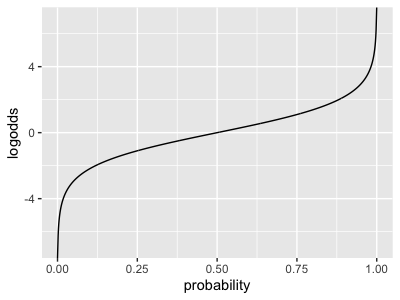
$\text{logit}()$ of course carries the unit inveral (x axis) back onto the real line (y axis).

Maths challenge

Show that $\text{logit}()$ and $\text{logistic}()$ are really inverse to each other. (Plug the expression for one into the expressino for the other, and simplify.)

(If you don't feel confident doing this maths, satisfy yourself that they are inverse to each other by trying some values in R.)

Interpreting estimates on the log-odds scale

If you follow this reasoning through, you'll see the following:

Interpretation

1. The linear predictor for each sample should be interpreted as the modelled log-odds that the sample is a disease case. (Transforming that through the logistic function, we get instead the modelled probability the sample is a disease case.

2. The parameters therefore represent the difference in log-odds associated with a unit increase in the predictor.

For example, in the above, $\beta$ indicates the difference in log-odds for individuals having O blood group, relative to those that don't.

Interpreting estimates on the odds scale

In between the probability scale and the log-odds scale, there is one more useful scale on which to interpret this. If we exponentiate the log-odds, we are in the odds scale. Exponentiation transforms sums to multiples and differences to ratios. Consequently $e^\beta$ ought to be the ratio of odds - the odds ratio - associated with a unit increase in the genotype.

To see this in practice, go back to the first fit (the one with no covariates). It looked like this:

summary(fit)$coeff

              Estimate Std. Error   z value    Pr(>|z|)
(Intercept)  0.1489326 0.02630689  5.661354 1.50183e-08
o_bld_group -0.3342393 0.03889801 -8.592709 8.49425e-18

The estimate for o blood group is $-0.334$. Now seperately, let's just make a table of the genotypes and outcomes:

table( data$status, data$o_bld_group )

           0    1
CONTROL 2690 2684
CASE    3122 2230

Let's think of this matrix as $\left(\begin{matrix} a & b \\ c & d\end{matrix}\right)$. One way to measure the difference in distribution of the two columns is to compute the odds in each column and take their ratio:

$$\text{odds ratio} = \frac{a/c}{b/d} = \frac{ad}{bc}$$

If you work this out for the above table you get:

odds_ratio = (2690*2230) / (3122*2684)

which works out to $0.7158825$.

Now for the magic trick:

exp( -0.3342393 )

[1] 0.7158825

Hey presto! Exponentiating the fitted parameter gives us the odds ratio, as expected.

Interpretation

Exponentiating the parameter estimates gives the odds ratio associated with a unit increase in each predictor.

Note

If you add covariates in there, you won't get exactly the same answer any more - your estimate is conditional on the other covariates. However, it's still usefully interpretable as a log odds ratio in this way.

A/B/O blood groups and malaria

From these data it certainly looks like O blood group is associated with severe malaria outcomes. But what about A/B blood group?

Including the variants as seperate predictors

What about the other SNP, rs8176746? This one encodes A/B blood type, with a 'T' allele encoding 'B' blood type and the 'G' allele (which the reference sequence carries) encoding 'A' blood type.

To look at this, we could of course just put the A/B SNP in the model instead. Let's encode as an additive model for simplicity:

data$rs8176746_dosage = NA
data$rs8176746_dosage[ data$rs8176746 == 'G/G' ] = 0
data$rs8176746_dosage[ data$rs8176746 == 'G/T' ] = 1
data$rs8176746_dosage[ data$rs8176746 == 'T/T' ] = 2
fit5 = glm(
    status ~ rs8176746_dosage + country,
    data = data,
    family = "binomial"  # needed to specify logistic regression
)
summary(fit5)$coeff

                    Estimate Std. Error    z value     Pr(>|z|)
(Intercept)      -0.07304875 0.03118217 -2.3426452 1.914758e-02
rs8176746_dosage  0.17814569 0.03573289  4.9854826 6.180734e-07
(etc.)

Hey - rs8176746 looks associated as well! Is B blood type associated with higher risk?

However, what happens if we put them both in at once?

fit5b = glm(
    status ~ o_bld_group + rs8176746_dosage + country,
    data = data,
    family = "binomial"  # needed to specify logistic regression
)
summary(fit5b)$coeff

                    Estimate Std. Error    z value     Pr(>|z|)
(Intercept)       0.10396026 0.04122405  2.5218350 1.167444e-02
o_bld_group      -0.30265008 0.04505738 -6.7169930 1.855129e-11
rs8176746_dosage  0.04228134 0.04143095  1.0205255 3.074793e-01
(etc.)

Oh. Now rs8176746 doesn't look associated.

So what's going on?

One way to think about this is to think of what the baseline level in the regression is - that's the level of predictors that only gives the baseline linear predictor:

• For fit5, the baseline is everyone who has rs8176746 == G/G.
• For fit5b, however, the baseline is everyone who has rs8176746 == G/G and has non-O blood type.

Even though the two models look similar, they are measuring different things. In the first fit (fit5), the baseline group includes a bunch of people who have O blood type, but in the second fit it doesn't.

Encoding A/B/O directly

A better way to solve this problem is to encode the biologically relevant variable directly. The biology works as follows: each individual has two chromosomes, and each carries the determinant of either the A or B antigen. Each chromosome might also carry a the loss-of-function 'O' deletion. Based on this we can call A/B/O blood type as follows:

combined genotype  blood group phenotype
-----------------  ---------------------
    C/C  G/G               A
    C/C  G/T               AB
    C/C  T/T               B
    -/C  G/G               A
    -/C  G/T            B or A? (*)
    -/C  T/T               B
    -/-  G/G               O
    -/-  G/T               O
    -/-  T/T               O

The cell marked (*) is the only difficult one here - both variants are heterozygous and we don't know from this data how they associated together on the chromosomes. However, here we are helped by the fact that O blood type mutation almost always occurs on the 'A' type background (i.e. chromosomes with 'G' allele at rs8176746). You can see this by tabling the two variants:

table( data$rs8176719, data$rs8176746 )

      G/G  G/T  T/T
 -/- 4621  264    7
 -/C 2331 2244   60
 C/C  331  510  287

With a few exceptions, all type O individuals have G/G genotype at rs8176746; the heterozygous -/C individuals are also consistent with most O type haplotypes carrying the 'G' allele. For the sake of this tutorial we will therefore assume that these doubly-heterozygous individuals have B blood type. Let's encode this now:

data$abo_type = factor( NA, levels = c( "A", "B", "AB", "O" ))
data$abo_type[ data$rs8176719 == 'C/C' & data$rs8176746 == 'G/G' ] = 'A'
data$abo_type[ data$rs8176719 == 'C/C' & data$rs8176746 == 'G/T' ] = 'AB'
data$abo_type[ data$rs8176719 == 'C/C' & data$rs8176746 == 'T/T' ] = 'B'
data$abo_type[ data$rs8176719 == '-/C' & data$rs8176746 == 'G/G' ] = 'A'
data$abo_type[ data$rs8176719 == '-/C' & data$rs8176746 == 'G/T' ] = 'B'
data$abo_type[ data$rs8176719 == '-/C' & data$rs8176746 == 'T/T' ] = 'B'
data$abo_type[ data$rs8176719 == '-/-' ] = 'O'

...and fit it:

fit6 = glm(
    status ~ abo_type + country,
    data = data,
    family = "binomial"  # needed to specify logistic regression
)
summary(fit6)$coeff

The baseline is now, of course, 'A' blood type individuals.

Question

Is there any evidence that B, or AB blood type is associated with a different risk of malaria, compared to A?

A challenge question

If O blood group is really protective, we'd expect the effect to be reasonably consistent across different subsets of our data - say across countries.

Question

Examine this by creating a forest plot. It should have:

• one row per country
• on each row, plot the regression estimate just from that country
• Behind each point plot the 95% confidence interval as a horizontal line segment.

Hint. To do this you will need to re-run the regression restricting to the samples from each country - then find a way to extract those estimates and their standard errors into a data frame for plotting.

Are the estimates across countries consistent?

Note

The 95% confidence interval is obtained by going out 1.96 times the standard error in each direction from the point estimate:

$$\text{95\% CI} = \hat{\beta} \pm 1.96 \times \text{se}$$