Functions

So far so good - you can create variables and do computations. To do really useful things, though, you need to use functions.

In fact we've seen a few already: we used the seq(), sum() and plot() functions on this page.

These illustrate the general form for using a function, which is:

function_name_goes_here( function arguments go here )

The function does some computation, based on its arguments in the brackets, and 'returns' its result.

Examples

Square roots

For example let's compute the square root of 1,000:

> sqrt(1000)

Here sqrt is the function name and 1000 is the function argument.

Trigonometry

Or we could compute the sine of an angle:

> sin( pi/4 )

(The angle is expressed in radians, so pi/2 means 45 degreees.)

Functions with more than one argument

If the function takes two or more arguments, seperate them with commas:

> rep( 2, 5 )
[1] 2 2 2 2 2

Note. The rep() function stands for 'repeat'. It repeats its first argument as many times as its second argument.

Many values make light work

Functions, just like everything else, work on vectors. For example let's generate a sine curve:

> x = seq( from = 0, to = 2*pi, by = 0.01 )
> y = sin(x)
> print(y)

and plot it:

> plot( x, y, type = 'l' )

Named arguments

These examples also illustrate another feature of functions: named arguments. In this case plot() has an argument named type which you can specify by giving its name. Here, type='l' tells it to draw the result as a line.

Question

What do you get if you don't include the type='l' argument?

plot() actually has about a zillion arguments, but they all have names and most of them have default values, so you only have to specify the ones you want to change. For example another argument is xlab which specifies the x axis label:

> plot( x, y, type = 'l', xlab = "Angle in radians" )

Challenge

Give the plot a sensible y axis label (ylab) as well. And also get rid of the 'box' round the outside by setting the 'box type' to 'n' (bty='n').

Generating random numbers

There are loads of other functions. For example we could generate some random numbers between 0 and 1 using runif():

> runif( n = 10 )
 [1] 0.7972164 0.6796878 0.3802085 0.8871665 0.0827587 0.6847181 0.5019356 0.5859209
 [9] 0.5115309 0.1100913

(You'll get a different values of course - they're random.)

A natural thing to do with random numbers is histogram them:

> x = runif( n = 100 )
> hist( x )

Or we could compute their mean or average:

> mean(x)

Formatting strings

A very useful function is sprintf() which can be used to format numbers into strings. For example to convert the number 5 to a string:

> sprintf( "%d" % 5 )

The first argument is the format string, which here uses '%d' to say 'format a decimal integer here'.
The other arguments are the values to be formatted.

sprintf() is useful to do general formatting. For example, to list some filenames:

> sprintf( "/path/to/images/image%d.jpg", 1:10 )

Or to print out some diagnostics:

> n = 10
> k = 5
> sprintf( "There are %d ways to choose %d objects from a set of %d.", choose(n,k), k, n )

Getting help

At this point, you may be wondering how you find out what a function does or what its arguments are. This where the help system comes in.

E.g. let's use the help function to find out what runif does:

> ?runif

You'll see that runif is one of several functions for dealing with 'uniform' distributions (that is, where all values in a range are equally likely). And it has some other arguments that can be used to alter how it behaves.

Question

Have a look at the documentation now and see if you can make sense of it. How would you use runif to simulate 10 random numbers between 1000 and 2000?

R help files are a bit of a mixed bag - they tend to have lots of details, but aren't always easy to read. Still they are a good first port of call when you want to figure something out. If still confused, a web search might also help.

Another way to search the help is with the double question mark form:

> ??runif

This will show you anything in the documentation that matches 'runif' or something close to it - a lot of results! Somewhere in that list will be stats::Uniform which is the page we were just looking at.

Question

Look up the documentation for sin(), exp(), log(), or sqrt() How could you plot the cosine of an angle, the exponential or logarithm or square root of a number? Make sure you understand how this works.

Writing your own functions

Everything we're doing here is done by calling built-in functions to compute or plot some values. Built-in functions are great! But what if you want your own?

Well, this is easy too. For example, let's write a function that converts a string to lower case, and then repeats it twenty times:

> repeat_it = function( a_string ) {
    rep( tolower( a_string ), 20 )
}

Our function uses the tolower() built-in function to convert the case, and the rep() built-in function (read its help!) to repeat the string. Try it out:

> repeat_it( "Repeat this!" )

Of course this function is silly - what if we want to repeat it 100 times instead? Let's give the function a number_of_repeats argument:

> repeat_it = function( a_string, number_of_repeats = 20 ) {
    rep( tolower( a_string ), number_of_repeats )
}

Question

Make sure you know how to call this function to repeat a string (say) twice or a hundred times.
What happens if you repeat a million times?

Functions like this work just like built-in functions, but you get to write them yourself. They are defined using the function keyword followed by a list of arguments inside brackets (). The *body of the function (i.e. the code it runs) goes straight afterwards, in between curly braces {}. Then the function returns the value of the last statement.

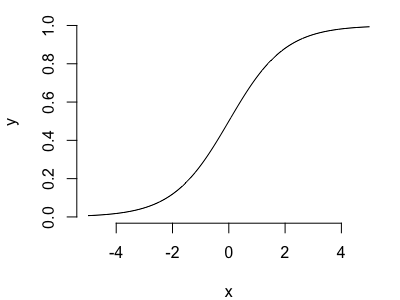
Example: the logistic function

Let's use our skills to plot the logistic function. It maps the real numbers into [0,1] and is defined as

$$x \mapsto \frac{e^x}{1+e^x}$$

In R we can define it as:

> logistic = function(x) {
    exp(x) / ( 1 + exp(x) )
}

Challenge

Plot the logistic function over a range from -5 to 5.

Hint. Create a variable x with a range of values from -5 to 5 using the seq() function. Then create a variable y with the values of the logistic function applied to x. Finally, plot y against x.

For maximum kudos your plot should be drawn as a line, have nice axis labels and no 'box' around it! So it should look something like this: